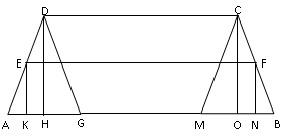
---

 

draw DG line so that DG||BC

draw CM line so that CM||AD

here, AB,BC,CD,DA are given.

DG=BC(known)

CM = AD (Known)

BG = CD (Known)

AG  = AB – BG = AB –CD (Known)

let,

CO = DH = H (Unknown)

FN = EK = h (Unknown)

In ΔADG

S=(AG+DG+AD)/2

area of ΔADG =(S * (S – AD) + (S – AG) * (S – DG) =A (known)……… (1)

area of ΔADG=(1/2)* AG * DH =(1/2)* AG * H ……………………..(2)

From equation (1) & (2) we get ,

(1/2)* AG * H=A

=>H=(2*A)/AG

Area of trapezium ABCD= 2*Area of trapezium ABFE=2*Area of trapezium EFCD

Area of trapezium ABCD=Area(known)

Area of trapezium ABFE= (AB + EF) * EK = (AB + EF) * h

Area of trapezium EFCD=(EF + CD) (DH – Ek) = (EF + CD) (H – h)

Area = 2 * (AB + EF) * h ……………….(3)

Area = 2 * (EF + CD) (H – h) ……………(4)

From (3) =>

h=Area/(2*(AB+EF))……………..(5)

putting the value of h in equation (4)

Area = 2 * (EF + CD) * {H – Area/(2*(AB+EF))  }

=> Area (AB + EF) = (EF + CD) * {2H * (AB + EF) – Area}

=>   Area * AB + Area * EF = EF * 2H * AB + 2H * EF² + AB * 2H*CD + 2H * CD * EF – Area * EF – Area * CD

=>     2H * EF² + (2H * AB + 2H * CD – 2 Area) EF + (AB * 2H * CD – Area * CD – Area * AB) = 0

=>   aEF² + bEF + c = 0

where,

a       = 2H

b       = 2H * AB + 2H * CD – 2 Area = 2H (AB + CD) – 2 Area

= 2Area – 2 Area = 0

c        = AB * 2H * CD – Area * CD – Area * AB

= AB*CD*2H – Area(AB+CD)

= AB*CD*2H – (AB+CD)*H(AB+CD) [GLv‡b  Area = (AB+CD)*H ]

= 2AB*CD*H –  (AB² +CD²)*H – 2AB*CD*H

=  – (AB²+CD²)*H

so, aEF² + bEF + c = aEF² + c =0 [hence b=0]

=>EF² = –c/a

Here the negative value of EF will not be accepted.

putting the value of EF in equation (5) we can calculate the value of h.

In equiangular triangles ΔAEK & ΔADH we get,

AE/AD=EK/DH

=>AE=(EK/DH)*AD

=>AE=(h/H)*AD

Again , in equiangular triangles ΔCOB & ΔBFN :

BF/BC=FN/CO

=>BF=(FN/CO)*BC

=>BF=(h/H)*BC

#include<stdio.h>
#include<math.h>

int main()
{

  int test, t, i;

  double ab, cd, bc, ad, a, b, c, s, AE, BF;

  scanf("%d", & test);

  t = test;

  i = 0;

  while (test)

  {

    scanf("%lf%lf%lf%lf", & ab, & cd, & ad, & bc);

    a = ab - cd;

    b = ad;

    c = bc;

    s = (a + b + c) / 2;

    double triangle_Area = sqrt(s * (s - a) * (s - b) * (s - c));

    double H;

    H = (2 * triangle_Area) / a;

    double x, z;

    double trapizium_area = (ab + cd) * H;
    x = 2 * H;

    z = -(ab * ab + cd * cd) * H;

    double ef = sqrt(-z / x);
    double h = trapizium_area / (2 * (ab + ef));

    AE = (h * ad) / H;

    BF = (h * bc) / H;

    printf("Land #%d: %lf %lf\n", i + 1, AE, BF);

    i++;

    test--;

  }
  return 0;

}

 

---

Next Previous